| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 잠실새내 도그존
- 화이트 해커를 위한 웹 해킹의 기술
- 고르드
- typescript
- graphql 400
- 홍대 예술
- 신촌 소문난집
- apollo react native
- 예쁜술집 예술
- apolloclient
- graphql mutation error
- 도그존
- 토라비
- promise메서드
- 화이트해커를 위한 웹 해킹의 기술
- 홍대 토라비
- graphql
- graphql react native
- 잠실새내
- promise처리
- 비동기배열
- 지보싶 신촌점
- 운정 소바동
- useMutation error
- 앙버터마카롱
- 홍대 카페 장쌤
- 금별맥주
- graphql with RN
- graphql with reactnative
- 비동기배열처리방법
- Today
- Total
yehey's 공부 노트 \n ο(=•ω<=)ρ⌒☆
[알고리즘] 시간복잡도 계산하기 본문
Today I Learned
: 내가 짠 해결 코드에서 시간복잡도 계산하고 예상 소요시간 예측하기
배경 / 이슈
5월부터 지금까지 주 3회 2문제씩 한 주에 약 6문제씩 알고리즘 문제를 풀어왔다. 지금까지는 백준, 코드트리(3*), 프로그래머스 등 다양한 플랫폼에서 알고리즘 준비를 해왔는데, 얼마 전에 현대오토에버 코딩테스트 준비로 소프티어에서 문제를 풀면서 준비했다. 그동안은 문제를 해결할 수 있는 알고리즘을 찾고 코드를 짜는 것에 초점을 맞췄다면 소프티어에서 문제를 풀면서는 다른 이슈로 인해 문제를 많이 틀렸다.
결과 값이 아예 오답인 것이 아니라 시간초과로 인해 문제를 많이 틀렸다. 물론 백준에서도 시간초과가 뜨는 경우가 많았지만, 그때는 아예 다른 알고리즘을 사용해야 풀리는 문제여서 시간초과에 대해 큰 고민을 하지 않았다.
한마디로 지금 이걸 공부하는 이유는 현대가 쏘아올린 작은 공.....

그동안은 감으로 완전탐색이 가능한지 아닌지를 알아냈다면 이제는 감이 아닌 수학적 계산으로 가능한지 아닌지를 알 수 있도록 공부해보자!!
Contents
시간 단위
우선 알고리즘을 풀다보면 시간이 주어진 경우가 많다.
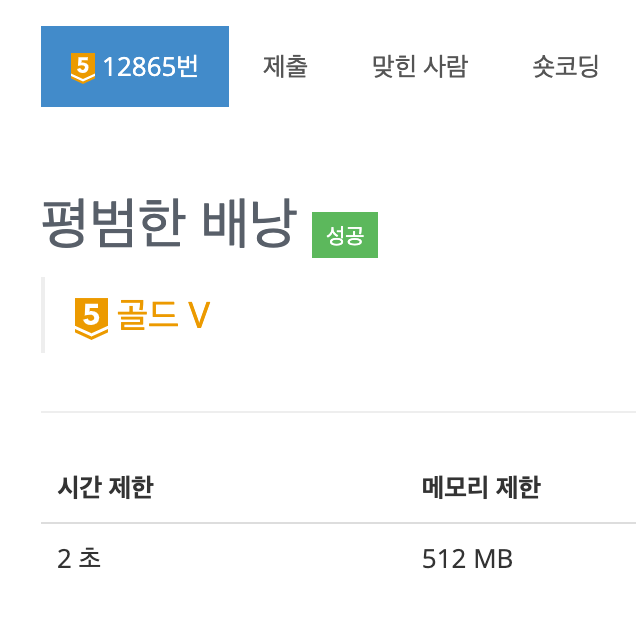
예컨대 위의 사진처럼 2초로 주어졌다면 테스트 케이스를 완료하는데 2초가 걸려야한다.
시간 복잡도를 계산하면서 가장 이해가 안갔던 부분이기도 하다.
보통은 내 로컬 컴퓨터의 vscode 에서 코드를 짜고 테스트를 진행하는데, 내 컴퓨터에서는 짱짱 빠르고 정확하게 돌아가기 때문에!!!
그치만 보통의 코딩테스트 연습 플랫폼에서는 다른 기준을 쓴다. 내 컴퓨터와 같은 사양을 제공하면 웬만하면 문제가 풀리기 때문..
그래서 1초의 시간에는 1억 + a 의 연산이 가능하다고 보면 된다. 여기서 a는 추가적인 연산으로 1억 500, 이정도는 1억으로 친다. (근데 일부의 경우 파이썬은 2000만번 연산이 가능하다고 하기도 한다...)
우리는 모든 연산을 계산하기에는 문제를 풀기에도 시간이 부족하다. 대략 잡아서 계산할 수 있어야하는데 여기서 Big O notation을 사용한다.
Big O notation
Big-O noatation은 알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도를 가진다는 의미이다.
예를 들어 f(x) = x^2 + 5x + 3 이라고 했을 때, 해당 f(x) 의 Big O notation 결과는 다음과 같다.
O(f(x)) = O(x^2 + 5x + 3) = O(x^2) 따라서 f(x)가 가지는 시간복잡도는 x^2 이다. (여기서 =는 완전 동일하다보다는 ~쯤 정도로 보면 됨)
따라서 풀이한 코드의 계산식(?)을 찾고, 그것의 Big O notation을 구해서 최악의 경우에 몇번의 연산이 수행되는지 계산 후 그것을 초로 나타내면 그게 소요시간이라고 볼 수 있다.
Practice
오늘 풀었던 문제 (계속 더 나은 방법은 없을지 고민하다가 도저히 찾을 수 없어서 구글링 햇다.ㅠ)
https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
#https://ryu-e.tistory.com/106 : 코드 출처
import sys
INF = int(1e9)
n = int(sys.stdin.readline()) # 도시의 수
m = int(sys.stdin.readline()) # 버스의 수
graph = [[INF] * (n + 1) for _ in range(n + 1)] # 모든 최단 거리를 저장
for i in range(1, n + 1):
for j in range(1, n + 1):
if i == j:
graph[i][j] = 0
for _ in range(m):
a, b, c = map(int, sys.stdin.readline().split())
graph[a][b] = min(c, graph[a][b]) # 노선이 하나가 아닐 수 있음 > 최소값 넣기
# 2. 다이나믹 프로그래밍
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
for a in range(1, n + 1):
for b in range(1, n + 1):
if graph[a][b] == INF:
print("0", end=" ")
else:
print(graph[a][b], end=" ")
print()여기서 f(x) 를 구해보자. 우선 단순 연산들은 최대한 계산하지 않는 방향으로 간다. (하나하나 계산해도 big - o 에서 다 사라질 예정)
f(x) = x^2 + x + x^3 + x^2 = x^3 + 2x^2 쯤으로 볼 수 있다.
여기서 O(f(x)) = x^3 이다.
x가 될 수 있는 최악의 경우의 수는 x=100 이므로 O(f(3)) = 100^3 = 1000000 으로 약 100만이다.
해당 문제의 시간제한은 1초고 1초동안은 약 1억의 연산을 수행할 수 있기 때문에 위의 문제는 3중 for문을 사용해도 시간 초과 없이 해결할 수 있는 것이다. (만약 n의 범위가 1000이었으면 불가능)
2번째 문제
https://www.acmicpc.net/problem/10942
10942번: 팰린드롬?
총 M개의 줄에 걸쳐 홍준이의 질문에 대한 명우의 답을 입력으로 주어진 순서에 따라서 출력한다. 팰린드롬인 경우에는 1, 아닌 경우에는 0을 출력한다.
www.acmicpc.net
import sys
N = int(sys.stdin.readline())
Arr = list(map(int,sys.stdin.readline().split()))
# R_Arr = reversed(Arr)
M = int(sys.stdin.readline())
def dp():
DP=[[0 for _ in range(N)] for _ in range(N)]
for i in range(N):
DP[i][i]=1
for i in range(N-1):
if Arr[i]==Arr[i+1]:
DP[i][i+1]=1
for cnt in range(N-2):
for i in range(N-2-cnt):
j = i+2+cnt
if Arr[i]==Arr[j] and DP[i+1][j-1]==1 :
DP[i][j]=1
return DP
DP = dp()
for _ in range(M):
s,e = map(lambda x: int(x)-1, sys.stdin.readline().split())
print(DP[s][e])
# check(s,e)
여기서도 f(x) 를 구한다. f(x) = x + (x-1) + (x-2)(x-2-i) + M O(f(x)) = x^2
최악의 경우 N = 2000이므로 4000000 이 최악의 연산 횟수라고 가정할 수 있다.
주어진 시간은 pypy3 기준 1.5초 이므로
4000000 < 30000000 으로 시간초과는 발생하지 않는다.
Learned
코드에서 Big O notation을 적용해서 시간복잡도와 시간초과 발생여부를 계산하는 방법을 알 수 있게 되었다.
앞으로는 시간초과를 생각하며 문제를 풀 수 있음!
What I Will Study
DFS, BFS 등 특수한 상황에서 자주 사용하는 알고리즘들의 시간복잡도에 대해서 공부할 예정
참조
https://noahlogs.tistory.com/27
빅오 표기법 (big-O notation) 이란
컴퓨터 과학(Computer Science) 에서 알고리즘은 어떠한 문제를 해결하기 위한 방법이고, 어떠한 문제를 해결 하기 위한 방법은 다양하기 때문에 방법(알고리즘) 간에 효율성을 비교하기 위해 빅오(bi
noahlogs.tistory.com
[자료구조] 빅오 표기법(Big-O notation)이란?
빅 오 표기법(Big-O notation)의 정의Big-O(또는 Big-Oh) notation은 알고리즘의 시간 복잡도를 나타내는 표기법이며, O(f(n))으로 나타낸다. 알고리즘의 시간 복잡도알고리즘의 복잡도를 판단하는 척도로는
holika.tistory.com
'알고리즘' 카테고리의 다른 글
| [백준] 16198번 에너지 모으기 (1) | 2021.07.17 |
|---|
